1. Примеры построения мат модели и канонич задачи ЛП.

Пример:

Предположим, что предприятие выпускает 2 вида продукции P1 P2. используя, при этом 3 вида ресурса S1, S2, S3. Запас ресурса, а также кол-во ед ресурса затрачиваемое на изготовление ед продукции приводится в след таблице <табл> . Реализация одной ед прод P1 приносит прибыль в 5уе. P2 – 7уе. Необходимо выяснить в каком кол-ве необходимо вып-ть прод P1 P2, чтобы прибыль была наибольшей. Необходио составить экономико-мат модель этой задачи. X1 – кол-во ед продукции P1, кот необходимо выпустить. X2 – P2. Тогда для изготовления указанных обоих видов продукции необходимо ресурсов в кол-ве: <сис-ма неравенств> (1) В силу ограниченности запасов ресурсов должна выполняться эта сис-ма. (2) x1≥0 x2≥0 Суммарная прибыль которой может быть получена при реализации всей продукции F=…

Таким образом, задача свелась к нахождению x1 x2, удовлетворяющих нерав-вам (1) (2) при кот фция F принимает наиб значение.

Общая постановка задачи ЛП:

Общей задачей ЛП нзв задача нахождения X=(x1, …, xn), удовлетворяющего (1) (2) (3) при кот (4) приним оптимальное значение.

Канонич задача ЛП нзв задача нахождения X=(x1, …, xn), удовлетворяющего (1) (3) при кот (4) оптимальна.

Стандартная задача ЛП нзв задача нахождения X=(x1, …, xn), удовлетворяющего (2) (3) при кот (4) оптимальна.

X=(x1, …, xn), удовлетворяющий (1) (2) (3) нзв допустимым решением.

///Необходимо найти максимальную прибыль или минимальные затраты при наличии некоторых реальных экономич, временных, трудовых ограничений. С мат точки зрения выше сказанное означает нахождение максимума и минимума функции многих переменных. (1) f(x1, …, xn) -> max (min) когда на эти переменные накладываются некоторые ограничения (2) j(x1, …, xn) ≤(≥, =)bi, i=(i, m). (1)-целевая функция (2)-ограничение.

Задачи подобного рода решаются с помощью экономико-мат методов в экономике.

Если фции, входящие в (1) и (2) имеют лин характер, то применяются методы так называемого лин программирования. Если же хотя бы одна из ф-ций имеют не лин вид, то прим-ся методы не лин программ. Если решение требуется в целых числах, то прим-ся методы целочисленного программирования. ///  

2.Теорема о доп базисном решении в угловых точках.

Если сис-ма векторов А1, …, Аn содержит m лин независимых векторов А1, …, Аm, то допустимое базисное решение X=(x1, …, xn, 0, …,0) явл угловой точкой многоугольника решений. И наоборот: в каждой угловой точке многоуг-ка решений соответ-ет допустимое базисное решение

Точка нзв угловой, если она не явл внутр ни для какого отрезка целиком принадлежащего данному множ-ву.

4.Решение задач ЛП геометрическим методом.

Геметрич метод применяется лишь для задач с двумя переменными.

(1) ai1x1+ai2x2 ≥(≤)bi, i=1,m

(2) x1, x2≥0

(3) F=c1x1+c2x2 -> max (min)

Нерав-во (1) определяет некоторую полуплоскость с граничными прямыми

(4) ai1x1+ai2x2 =bi, i=1,m

Чтобы определить полуплоскость соответ-ую (1) , сначала строят прямую (4). Затем, берется любая точка, не лежащая на указанной прямой и подставляется в исходное нерав-во (1). Если точке удовл-ет (1) то (1) определяет полуплоскость, содержащую эту точку. Если не удовлетворяет, то определяет полупл-ть не содержащую эту точку.

Согласно основной теореме ЛП, если решение сущ-ет, то оно достигается либо в одной из вершин, образуемую выпуклой областью, либо во всех точках одной из его сторон. Находят это решение так: Строят градиент ф-ции F. N=gradn(dF/dx1, dF/dx2)=(c1, c2). Этот вектор показывает направление возрастающей функции F, а обратное направление – убывание. Затем, строится линия уровня ф-ции F (прямая перпенд-ая градиенту). Передвигая линию уровня вдость градиента можно получить один из след случаев: единств реш, альтернативн, неогр, несовместности ограничений(нет реш)

5.Симплексная таблица, нахождение нового базисного решения, признак оптимальности.

Для решения задачи, не имеющей предпочтительный вид необходимо составить М-задачу и получить предпочтит вид. Таким образом, любую задачу ЛП можно представить в след виде: (2)

Выразим из (2) xi:

Введем след обозначения:

Подставим xi в(1) и, сгруппировав получится задача в след виде: <симплекс таблица>

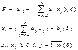
Dj – оценки Сб

Признак оптимальности доп базисного решения:

Если для некот допустимого базисного решении оценки Dj (за исключением D0) ³0 (£0), то такое базисное решение доставляет максимум(миним).

Переход к новому базису:

Рассмотрим задачу максимума. Если все Dj0>=0, то достигли цели. Пусть сущ-ет x0: сущ номер j0: Dj0<0. тогда вектор-столбец Аj0 нзв разрешающим, а переменная xj0 – перспективной. Можно увеличить значение ф-ции F засчет увеличения перм xj0. При увеличении xj0 необходимо учитывать неотриц-ть базисных переменных. Так как св прем = 0 и перспективные переменные неотрицательны, то xi=bi-aij0xj0 (i=1,m). Если aij0>0, то при значительном увеличении xj0 можем получить отрицат xi, что недопустимо. Пусть, первые к значений aij0>0. Тогда будем увеличивать xj0 до тех пор, пока xi>=0, т.е bi-aij0xj0>=0 => {xj0= bi/ aij0, aij0>0. Выберем среди правых частей наим долю. Пусть она достигается в строке i0, тогда эта строка – разрешающая, а элемент aij0 разреш-м элементом. Переведем базисную пременную xi0 в своб переем, а своб переем xj0 в базисную. Получаем новое допустимое базисное решение X1. Для этого выполняется D0-Dj0xi0=F(x0)-Dj0xi0>=F(x0)

3.Теорема о достижении экстремума значения целевой ф-ции в угловой точке.

Если задача ЛП имеет решение, то целевая ф-ция достигает экстемального значения хотя бы в одной из угловых точек многоугольника решений; если же целевая ф-ция достигает оптимального значения более, чем в одной угловой точке, то она достигает того же самого значения в любой точке, являющейся их выпуклой лин комбинацией.  

6.Сходимость симплексного метода.

Канонич задача ЛП нзв невырожденной, если все ее базисные решения невырождены, т.е ни одно из базисных переменных не имеет нулевого значения. Если среди базисных решений есть хотя бы одно вырожденное, то задача ЛП нзв вырожденной.

Так как при переходе от одной симплекс таблицы к другой используют правило прямоугольника, следоват-но значения целевых функций при нахождении максимума на двух последующих итерациях связаны формулой D0k+1=D0k-bi0Dj0/ai0jo (1)

bi0>=0, Dj0<=0, ai0jo>0. Если задача невырождена, то bi0>0, Dj0<=0 => D0k+1>=D0k, Т.е ф-ция F монотонно возрастает.

Теорема: Если все допустимые базисные решения задачи ЛП невырождены, то симплексным методом за конечное число итераций будет найдено либо оптимальное решение, либо будет установлена неограниченность целевой ф-ции.

7.Зацикливание, выход из цикла.

Если задача ЛП вырождена, то bi0=0 => D0k+1=D0k, Т.е. ы переходим к нехудшему допустимому базисному решению, но значение целевой ф-ции не изменится. Если такая ситуация будет систематически повторяться, при переходе к новому базисному решению, то в силу конечности доп-х базисных решений ы придем к решению, которое ранее встречалось, т.е будем иметь повторяющееся симплекс таблицу. Т.о. получили зацикливание. Зацикливание можно избежать изменением правила выбора завершающего столбца и строки.

К строке Qi симпл таблицы будем присваивать номер базисной переменной xi, соответствующий этой таблице. Qm+1=(D0, D1, …, Dn).

Допустимое базисное решение xi нзв обобщенно-положительным, если Qiý0 "iÎI={i1, …, im}.

Если x0 – допустимое баз решение, то сделать его обобщен-положительным можно перенумеровав столбцы матрицы А. В невырожденной задаче все допустимые базисн решения обобщ-положительны.

Пусть имеется задача на минимум, x0 – допуст баз решение.

Теорема: Если Dj0 >0, а индекс разрешающей строки i0 выбрать из множ-ва I’={iÎI: aij0>0} Так, чтобы 1/ai0j0Qi0í1/aij0Qi, i¹i0, то новое допустимое базисное решение будет обобщ-положит, при этом Q’m+1íQm+1

Вывод из теоремы: если перед решением задачи произвести нумерацию базисных переменных xi так, что исходное допуст баз решение будет обобщ-положит, а разрешающую строку при каждой последующей итерации выбирать по правилу (1), то зацикливания не произойдет. Это следует из того, что если сущ Dj0 >0, aij0>0 для некотор i, то при переходе к нов допустим базису строка Qm+1 будет лексикографически уменьшаться. Поэтому ни одно из допуст баз решений не повторится с исх допус баз решениями. А в силу конечности допуст баз решений получим, что найдется либо оптим решение, либо ф-ция F неограниченна снизу.

8. 1 метод искусственного базиса.

Пусть имеется канонич задача ЛП

Допустим, что все bi≥0. Ограничение в (1) имеет предпочтительный вид, если левая часть ограничения содержит переменную, входящую с коэф-ом =1, а в ост огранич-ях с коэф 0.

Если каждое ограничение в (1) имеет предпочтит вид, то допуст базисное решение находится путем приравнивания к 0 всех непредпочтит-х переменных. Если при этом получили не более m 0-ых координат, то согласно теореме об угловых точках многоуг-ка решений получим доп базисное решение. В этом случае предпочтит эл-ты есть базисные, а не предпочтит-ые – свободные.

А если не все ограничения имеют предпочтит вид, то в левую часть вводятся искусственные переменные Wi. В ф-цю F переменные Wi вводятся с коэф М в случае нахождения минимума, и с коэф-ом –М в случае нахождения максимума, где М – большое положит число. Полученная задача нза М-задачей соответ-ей исходной. М-задача всегда имеет предпочтит вид.

(2*)

Теорема: Если в оптимальном решении М-задачи X*(x1, …, xn, W1, …, Wn) все искуственнве преенные Wi =0, то решение X=(x1, …, xn) явл оптимальным и для исходной задачи.

9. 2 метод искусственного базиса.

Необх найти решение канонич задачи ЛП:

bi>=0, i=1,m; xj>=0, j=1, n (1)

(2)

Пусть (1) не имеет предпочтит вид. Вводим дп переменные Wn+1, …, Wn+m так, чтобы (1) приобрела предпочтит вид.

bi>=0, i=1,m; xj>=0, j=1, n (

4

)

Теорема:

Пусть задача (1) (2) имеет доп решение X=(x1, …, xnn, Wn+1, …, Wn+m) явл оптимальным для задачи (3) (4), ТТогда все искусств переем =0.

Алгоритм:

1.

Задача (1) (2) преобразуется в (3) (4) 2.

задача (3) (4) решается симплексным методом. Находят x. 3.

если x невырожден, то в посл симплекс таблице вычеркиваются столбцы, соответствующие искусственным переменным и пересчитывается Dj. Это будет исходна симплекс таблица для задачи (1) (2)  

10. Метод обратной матрицы

Идея: пусть исходный базис состоит из векторов A1, …, Am. Xi и ci соответствуют базисным векторам. В симплексном методе использовалась формула (1)

А в методе обратной матрицы запись векторов aij используется как Aб-1Aj. Оценки Dj можно записать в виде: Dj=Cб Aб-1Aj – cj (2)

Следоват-но сначала вычисляем вектор CбAб-1 , а затем уножаем его скалярно на столбец матрицы Aj.

Алгоритм:

1)

находим такой базис, чтобы базисное решение было допустимым, т.е Aб-1, В>=0, где В=(b1, …, bn). АБ=(А1, …, An). 2)

Находим U= CбAб-1 3)

из (2) находим Dj=UTAj – cj, j=1, n.

Если все Dj<=(>=)0, То получаем минимум(максимум). Задача решена и оптим решение равно Aб-1В. А если, например, при нахождении минимума некоторое Dj>0, то переходим к шагу 4. 4)

Находим вектор Aб-1Aj0, если все элементы этого вектора <=0, то целевая ф-ция неограничена снизу, а если хотя бы 1 >0, то переходим к шагу 5. 5)

Находим наименьшее из отношений значений bi вектора Aб-1В к положит- компонентам вектора Aб-1Aj0. Пусть оно достигается в компоненте j0, тогда новым базисом будет ‘Aб=(A1, …, Aб-1, Aj0, Ai0+1, …, Am). 6) находим ‘Aб-1. 7) переходим к шагу 2 с новой Aб-1

Для этих вычислений составляем след таблицы:

12. 1 теорема двойственности

Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение. Причем, F(x*)=z(y*). Если в одной из двойств-х задач целевая ф-ция ограничена, то сис-ма ограничений другой задачи противоречива.

Канонический смысл: план производства и оценки ресурсов оптимальны ТТогда цена производственной продукции и суммарная оценка ресурсов совпадает.

13. 2 теорема двойственности.

Или теорема дополняющей нечетности.

Решение x*, y* оптимальны ТТогда выполняется след условие: xj*(<сумма>aijyi*-cj)=0 j=1,n. (1)

yi*(<сумма>aijxj*-bi)=0 i=1,m (2)

Канонический смысл:

Из (1) (2) следует, что если какое либо ограничение одной из задач с компонентами оптимального решения обращается в строгое нерав-во, то соответствующая компонента оптимального решения двойственной задачи = 0. Если же компоненты оптимального решения одной из задач положительны, то соответствующие ограничения в двойственной задаче с компонентами оптимального решения должно обращаться в строгое неравенство, т.е <сумма>aijxj*<bi, то yi*=0, если же yi*>0, то <сумма> aijxj*=bi,. И аналогчно, <сумма>aijyi*<cj то xj*=0, если же xj*>0, то <сумма>aijyi*=cj

С Экономич точки зрения:

Если в некотором оптимальном решении расход ресурсов строго меньше его запаса, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса = 0. Если же в оптимальном плане производства расход соответствующего ресурса равен его запасу, то двойственные оценки служат мерой дефицитности ресурсов.

11. Лемма двойственности

Задачи (1) (2) называются взимодвойственными задачами.

Для любых допустимых решений X задача (1), и задача (2) выполняются: F(x)<=z(y) (3)

Док-во: f(x)=(сумма)cjxj<=<сумма> (<сумма>yiaij)xj=<сумма>yi(<сумма>aijxj) <=<сумма>yiai=z(y)

(3) – основное неравенство даойственности

14.3 теорема двойственности

Или теорема об оценках.

Двойственные оценки: yi*=dFmax(xn)/dbi, i=1,m Экономический смысл: